Given an unsorted array A of size N that contains only non-negative integers, find a continuous sub-array that adds to a given number S.
In case of multiple subarrays, return the subarray which comes first on moving from left to right.
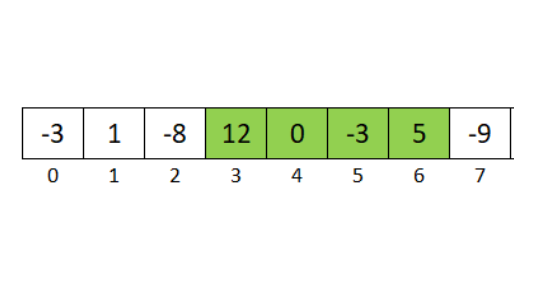
Example of Subarray Within Given Sum
Input:
N = 5, S = 12
A[] = {1,2,3,7,5}
Output: 2 4
Explanation: The sum of elements
from 2nd position to 4th position
is 12.
Input:
N = 10, S = 15
A[] = {1,2,3,4,5,6,7,8,9,10}
Output: 1 5
Explanation: The sum of elements
from 1st position to 5th position
is 15.
Approach
If the sum of a subarray exceeds the given sum, adding elements to the current subarray will not result in the sum becoming x. (given sum). The concept is to use a sliding window-style technique. Begin with an empty subarray and gradually add elements until the sum equals x. Remove entries from the current subarray’s beginning if the sum is bigger than x.
Code for Subarray Within Given Number
- Initialize curr_sum as value of the first element
- The starting point as 0
- Add elements one by one to curr_sum and if the curr_sum exceeds the sum, then remove starting element.
- If curr_sum exceeds the sum, then remove the starting elements.
- If curr_sum becomes equal to the sum, then return start and end positions.
Python Code
#function to check subarray
def checkSubArraySum(arr, n, sum):
# Initialize curr_sum as value of first element
# starting point as 0
curr_sum = arr[0]
start = 0
ans = []
# Add elements one by one to curr_sum and if the curr_sum exceeds the sum, then remove starting element
i = 1
while i <= n: # If curr_sum exceeds the sum, then remove the starting elements while curr_sum > sum and start < i-1:
curr_sum = curr_sum - arr[start]
start += 1
# If curr_sum becomes equal to sum, then return true
if curr_sum == sum:
ans.append(start+1)
ans.append(i)
return ans
# Add this element to curr_sum
if i < n:
curr_sum = curr_sum + arr[i]
i += 1
# If no subarray return -1
ans.append(-1)
return ans
arr = [15, 2, 4, 8, 9, 5, 10, 23]
n = len(arr)
sum = 21
print(checkSubArraySum(arr, n, sum))
Complexity Analysis:
Time Complexity: O(n)
Space Complexity: O(1).